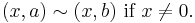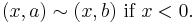Non-Hausdorff manifold
In mathematics, it is a usual axiom of a manifold to be a Hausdorff space, and this is assumed throughout geometry and topology: "manifold" means "(second countable) Hausdorff manifold".
In general topology, this axiom is relaxed, and one studies non-Hausdorff manifolds: spaces locally homeomorphic to Euclidean space, but not necessarily Hausdorff.
Contents |
Examples
Line with two origins
The most familiar non-Hausdorff manifold is the line with two origins, or bug-eyed line.
This is the quotient space of two copies of the real line
- R × {a} and R × {b}
with the equivalence relation
This space has a single point for each nonzero real number r and two points 0a and 0b. In this space all neighbourhoods of 0a intersect all neighbourhoods of 0b, so it is non-Hausdorff.
Further, the line with two origins does not have the homotopy type of a CW-complex, or of any Hausdorff space[1].
Branching line
Similar to the line with two origins is the branching line.
This is the quotient space of two copies of the real line
- R × {a} and R × {b}
with the equivalence relation
This space has a single point for each negative real number r and two points 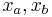 for every non-negative number: it has a "fork" at zero.
for every non-negative number: it has a "fork" at zero.
Etale space
The etale space of a sheaf, such as the sheaf of continuous real functions over a manifold, is a manifold that is often non-Hausdorff. (The etale space is Hausdorff if it is a sheaf of functions with some sort of analytic continuation property.)
Notes
- ^ Gabard, pp. 4-5
References
- Baillif, Mathieu; Gabard, Alexandre, Manifolds: Hausdorffness versus homogeneity, arXiv:math.GN/0609098v1
- Gabard, Alexandre, A separable manifold failing to have the homotopy type of a CW-complex, arXiv:math.GT/0609665v1